 Allgemeine und Anorganische Chemie (AC1)
Allgemeine und Anorganische Chemie (AC1) In der Lewis-Schreibweise und der damit verknüpften Valenzbindungsmethode (VB-Methode) wird ein Molekül bevorzugt aus 2e-2z-Bindungen aufgebaut. Wird eine elektronische Situation nur unvollkommen durch ein über zwei Zentren gleichverteiltes Orbital beschrieben, werden Resonanzformeln eingesetzt, um den jeweiligen Zustand zutreffender zu umschreiben. So kann eine polare kovalente Bindung durch Mesomerie zwischen einer kovalenten Zweizentrenbindung und einer ionischen Grenzformel beschrieben werden oder eine 4e-3z-Bindung durch zwei Formeln, in denen ein kovalenter und ein ionischer Beitrag die Plätze wechseln.
Molekülorbitale beschreiben die elektronische Struktur eines Moleküls scheinbar auf völlig andere Weise. Oft umfasst ein MO alle Zentren des betrachteten Moleküls. So stellen die Orbitale ψ1, ψ2 und ψ3 im MO-Schema des H2S-Moleküls 2e-3z-Zustände dar. Nur ψ4 ist allein am S-Atom zentriert und entspricht einem der freien Elektronenpaare der Lewisformel.
Um Experimente zu deuten, die das gesamte Molekül betreffen (Elektronenspektren, Redoxvorgänge, magnetische Phänomene), sind MO-Schemata alternativen Betrachtungsweisen oft überlegen. Bei Fragestellungen, bei denen die individuelle Bindung zwischen zwei Atomen oder ein freies Elektronenpaar an einem individuellen Atom im Vordergrund steht (Schwingungsspektren, Acidität und Basizität, Nukleophilie und Elektrophilie), erleichtert es die Vorstellung nicht gerade, dass zum Beispiel bei H2S drei MOs zu jeder der beiden H-S-Wechselwirkungen beitragen (ψ1–ψ3). Im Folgenden wird daher zuerst das Ergebnis eines Lokalisierungsverfahrens vorgestellt, mit dessen Hilfe MOs in Orbitale umgewandelt werden können, die an einem Atom oder zwischen zwei Atomen lokalisiert sind. Anschließend wird erläutert, wie dies geschieht. Zuerst also das Ergebnis einer Lokalisierungsrechnung für das H2S-Molekül:
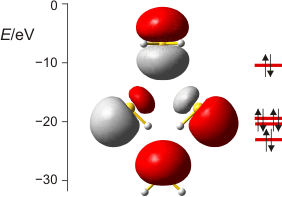
Vier gefüllte, lokalisierte Valenzorbitale im H2S-Molekül; von unten nach oben: freies e-Paar an S mit ca. 70 % 3s-Charakter, zwei entartete 2e-2z-Bindungen mit jeweils 15 % S(3s)-Anteil, freies p-Elektronenpaar. Bei den unteren drei Orbitalen ist der Blick auf die Ebene der drei Atome gerichtet, beim oberen senkrecht dazu. (Techn. Anm.: mp2/aug-cc-pvqz + nbo).
Ausgehend von einer Lewis-Formel erscheint das Ergebnis unmittelbar anschaulich: das stabilste Orbital hat weitgehend S(3s)-Charakter. Auf der Energieskala folgen die beiden S-H-Bindungen, zu denen die Wasserstoffatome jeweils ihr 1s-Orbital beitragen, während das Schwefelatom zwei seiner p-Orbitale einsetzt. Zur Bindungsverstärkung (siehe unten) setzt das Schwefelatom dabei keine reinen p-Obitale ein, sondern Orbitale, die zu 85 % 3p- und zu 15 % 3s-Charakter haben. Das energiereichste Orbital ist das zweite freie Elektronenpaar am Schwefelatom, es ist ein reines S(3p)-Orbital.
Welche Überlegung liegt einer solchen Neuformulierung der Valenzelektronenanordnung zugrunde? Man erinnere sich, dass die MOs durch Linearkombination von Atomorbitalen (AOs) zustande kamen. Es ist nicht Gegenstand dieser Vorlesung, die Regeln zu behandeln, nach denen die hier gezeigten „kanonischen Molekülorbitale“ zu bilden sind – es sind die Regeln der Symmetrielehre. Wir wollen es jedoch als plausibel ansehen, dass durch Linearkombination von AOs und MOs auch andere, gleichwertige, Beschreibungen einer Elektronenanordnung möglich sind. In diesem Sinne zeigt das folgende Bild das Ergebnis einer Linearkombination der MOs ψ2 und ψ3 aus dem MO-Schema des H2S-Moleküls:

Es wird deutlich, dass die Addition von ψ2 und ψ3 ein entlang der im Bild rechten S-H-Bindung lokalisiertes Orbital erzeugt. Addition von ψ1in dem geringen Umfang, zu dem dieses vor allem schwefelständige MO zu den S-H-Bindungen beiträgt, führt zum abgebildeten lokalisierten Orbital, das eine der beiden Bindungen beschreibt. Auf dieselbe Weise wird die zweite 2e-2z-Bindung durch Linearkombination von MOs erzeugt.
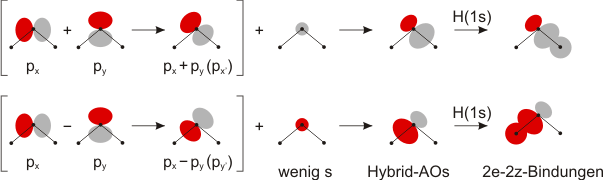
Da MOs durch Linearkombination von AOs gebildet werden, lässt sich dieses Ergebnis auch in der Sprechweise der VB-Theorie darstellen. Hier wird die räumliche Ausrichtung der Orbitale und der s/p-Anteil zuerst für jedes Atom eingestellt. Die Bildung der Bindung ist dann der letzte Schritt. Die folgende Abbildung geht dabei zum besseren Vergleich von denselben Koordinatenachsen aus wie beim MO-Schema. Dies ist möglich, da durch Linearkombination auch Achsentransformationen dargestellt werden können (im Bild: man hätte bei H2S naheliegenderweise auch von den Richtungen x' und y' ausgehen können). Durch passende Kombination von p-AOs und demselben s-Anteil wie bei der MO-Behandlung entstehen Hybridorbitale. Deren Kombination mit den H(1s)-AOs führt zu den beiden Bindungen in H2O und H2S:
Das einfache VSEPR-Modell geht weder davon aus, dass der optimale s-Anteil variabel ist, noch wird ein Unterschied zwischen der Hybridisierung freier Elektronenpaare und Bindungselektronen gemacht. Nachdem wir nun als Ergebnis einer quantitativen Behandlung für die Bindungen im H2S-Molekül einen s-Anteil von 15 % erhalten haben, stellt sich die Frage nach der Formulierung der beiden freien Elektronenpaare. Hierzu folgen wir der einfachen Näherung: s-Orbitalanteile dienen zur Verstärkung einer Bindung (indem sie den auf den Bindungspartner ausgerichteten Lappen eines p-Orbitals vergrößern). Ist der hierzu eingesetzte s-Anteil bekannt, sind zwei prinzipielle Vorgehensweisen möglich, die beide in geläufigen Rechenalgorithmen der Computerchemie realisiert sind: (1) der verbliebene s-Anteil wird gleichmäßig mit dem verbliebenen p-Anteil zu Hybridorbitalen kombiniert oder (2) es wird ein möglichst reines s-Orbital und ein möglichst reines p-Orbital formuliert. Das letztere Verfahren ist bei der in diesem Skript durchgängig angewandten Lokalisierungsmethode (der sog. NBO-Analyse) implementiert.
Bei H2S führt die zweite Methode zu folgendem Ergebnis: das pz-Orbital wurde nicht zur Formulierung der Bindung herangezogen – dieses stellt ein freies p-Elektronenpaar dar (in der Abbildung oben das energiereichste Orbital). In der x-y-Ebene bleibt nach Bildung der Bindungen „übrig“: 2 × 15 % p und 70 % s. Kombiniert ergibt sich das zweite freie Elektronenpaar als s-Orbital, das durch einen 30-%-igen p-Anteil von den Bindungen weggedrängt ist – auch dies geht aus der Abbildung unmittelbar hervor.
Lokalisierung der in Teil A gezeigten MOs des freien Wassermoleküls führt zu folgendem Schema, in dem wieder leicht die Lewis-Formel erkannt werden kann:
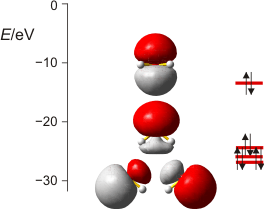
Vier gefüllte, lokalisierte Valenzorbitale im H2O-Molekül; von unten nach oben: zwei entartete 2e-2z-Bindungen mit jeweils 24 % O(2s)-Anteil, freies e-Paar an O mit 52 % 2s-Charakter, freies p-Elektronenpaar. Bei den unteren drei Orbitalen ist der Blick auf die Ebene der drei Atome gerichtet, beim oberen senkrecht dazu. (Techn. Anm.: mp2/aug-cc-pvqz + nbo).
Der Unterschied zu Schwefelwasserstoff besteht vor allem im höheren s-Anteil der Bindungen, der nun 24 statt 15 % beträgt. Als Folge weist das stabilere freie Elektronenpaar nun einen p-Anteil von fast 50 % auf. Es ist nicht mehr, wie beim H2S, das stabilste Orbital überhaupt und es weist aufgrund des p-Anteils weiter in den Raum hinaus – auf die Folgen für die chemischen Eigenschaften werden wir beim Paar NH3/PH3 eingehen.
Die Betrachtung lokalisierter Bindungen haben als merklichen Unterschied zwischen Wasser und Schwefelwasserstoff verschiedene s:p-Anteile bei den Bindungen und beim stabileren freien Elektronenpaar gezeigt. Erklärt dies zufriedenstellend die beobachteten Bindungswinkel? Um dies zu prüfen, muss der Winkel zwischen den Achsen der betreffenden Hybridorbitale für die jeweilige Hybridisierung berechnet werden. Dies gelingt, wenn die Orbitale eines Atoms so formuliert werden, dass – unter Berücksichtigung der Vorzeichen der Orbitallappen – keine Netto-Überlappung vorliegt (wenn die Orbitale „orthogonal“ sind). Unter dieser Randbedingung entspricht ein 25-%-iger s-Anteil einem Bindungswinkel von 109,5° (dem „Tetraederwinkel“), ein 33,3-%-ger Anteil einem 120°-Winkel. Für Wasser ist der errechnete Winkel zwischen den Achsen der Bindungsorbitale des Sauerstoffatoms ca. 6° größer als der experimentell bestimmte H-O-H-Winkel, für Schwefelwasserstoff ist der Orbitalwinkel um ca. 5° größer als der fast rechte H-S-H-Winkel. Die Differenz der Bindungswinkel in H2O und H2S ist also mit dem unterschiedlichen s(E)-Anteil in den H-E-Bindungen korreliert. Es bleibt die Frage, warum in beiden Molekülen der H-E-H-Winkel gegenüber dem Winkel zwischen orthogonal formulierten Bindungselektronenpaaren verkleinert ist.
Die Ursache der Orbitalverzerrung wird deutlich, wenn alle Valenzorbitale der beiden Moleküle betrachtet werden. Dies ist im folgenden Schema dargestellt. Die Orbitale sind maßstabsgerecht dargestellt und alle gleichermaßen bei einem höheren Funktionswert konturiert als bei den bisherigen Darstellungen – sie wirken also kleiner (das freie p-Orbital ist nicht berücksichtigt; man mache sich klar, dass dessen Wechselwirkung mit den übrigen drei Valenzorbitalen nicht vom Bindungswinkel abhängt):

Wird von einer gegenseitigen Abstoßung zwischen den Valenzelektronenpaaren ausgegangen, so geht aus beiden Abbildungen hervor, dass diese in den Molekülstrukturen ausbalanciert ist. Wäre beim links dargestellten Wassermolekül der Bindungswinkel kleiner, würden sich die schwarz dargestellten Bindungselektronenpaare stärker abstoßen, wäre er größer, würde die Abstoßung zwischen Bindungselektronenpaaren und dem rot gezeichneten freien Elektronenpaar größer.
Der geringere s-Anteil der Bindungen und der höhere Anteil im freien s-Elektronenpaar des Schwefelwasserstoff-moleküls lässt sich unmittelbar ablesen: sowohl das freie Elektronenpaar als auch die Bindungselektronen sind im Bild nach unten verschoben – ersteres hin zum S-Rumpf, letztere von ihm weg. Ungefähr gleich große Durchdringungsbereiche ergeben sich, wenn wie beim Wassermolekül der Bindungswinkel um einige Grad weiter verkleinert wird.
Fassen wir zusammen: Um die Struktur des H2S-Moleküls vorherzusagen, gehen wir von der Elektronenkonfiguration der beteiligten Atome in deren Grundzustand aus, also von 2 H-Atomen mit 1s1-Konfiguration und einem Schwefelatom mit der Konfiguration [Ne]3s23px23py13pz1. Anschließend werden im Einklang mit der Oktettregel zwei kovalente Bindungen aufgebaut. Schwefel verwendet hierzu p-Orbitale, der erwartete Bindungswinkel ist damit 90°. Verglichen mit dem experimentell ermittelten Wert von 92° ist zunächst kein Bedarf erkennbar, tiefer in eine bindungstheoretische Behandlung einzusteigen – wenn nicht der Vergleich mit dem Wassermolekül wäre.