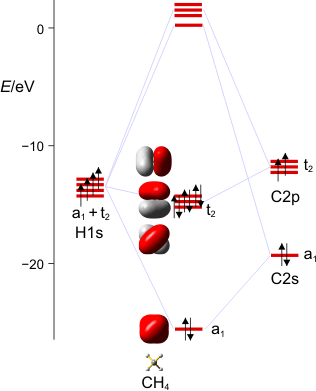
Das MO-Schema von Methan (als pdf):
2 SWS, Do 11–13, online als Zoom-Meeting,
Beginn: 4. Juni 2020, Ende: 6. August 2020 (9 Doppelstunden).
In diesem Semester ist auch hier alles anders. Da eine Präsenzveranstaltung nicht möglich ist, wurden Sie per E-Mail zu einem Zoom-Meeting eingeladen. Im Meeting gebe ich dann den Bildschirm für eine pdf-Datei frei, die im Laufe der Vorlesung mit dem Text ergänzt wird, der normalerweise an die Tafel geschrieben wird. Nach jeder Doppelstunde wird die ergänzte Datei ebenfalls zum Herunterladen bereitgestellt. Für beide Dateien brauchen Sie ein Passwort, das ich Ihnen bei der Zoom-Einladung mitgeteilt habe.
Die Vorlesungszeit ist zweimal 45 Minuten, wir machen also von 12:00 bis 12:15 eine Pause. Während dieser Pause läuft die Schaltung einfach weiter, so dass Sie die Chatfunktion benutzen können, um weitere Fragen zu stellen. Umgekehrt versuche ich auch Fragen an Sie zu stellen, die Sie dann beantworten können. Melden Sie sich doch bei Zoom bitte mit Ihrem vollen Namen an, dann kann ich Sie aufrufen.
Beachten Sie für alle Fragen rund um das Speichern und Weiterverbreiten der präsentierten Inhalte einen rechtlichen Hinweis.
Lehramtstudium Chemie: Studierende im Hauptstudium. Die Vorlesung ist die Begleitveranstaltung zum "LAF-Praktikum". Die Veranstaltung soll für ein tieferes Verständnis der Dinge sorgen, die im Praktikum beispielhaft angesprochen werden. Während die modernen Untersuchungsmethoden in praktikumsbegleitenden Seminaren vorgestellt werden, geht es in der Vorlesung um Konzepte (chemische Bindung, Ablauf und Thermodynamik von Reaktionen, Prinzipien bioanorganischer und organometallchemischer Umsetzungen).
Die Klausur zum LAF-Praktikum findet am Donnerstag, dem 13. August 2020, statt (weitere Angaben in Kürze). Studierende, die an dieser Klausur teilgenommen, aber mit der Note „mangelhaft“ nicht bestanden haben, haben die Möglichkeit, am Montag, dem 12. Oktober 2020, an einer Wiederholungsklausur teilzunehmen. Für beide Klausuren ist die Anmeldung über das LSF Voraussetzung.
Die Vorlesung greift typischen Grundvorlesungsstoff auf, da dort viele Themen angeschnitten werden, die auch schulrelevant sind. Naturgemäß wird dabei aber um etliche Lehrinhalte ein Bogen gemacht, die dem Fortgeschrittenen-Unterricht zuzuordnen sind. Ein Beipiel: die MO-Theorie lässt sich mit Kenntnis der Atomorbitale des Kohlenstoffs prima auf Methan anwenden, da sich in diesem geschickt ausgewählten Fall die Valenzorbitale des C-Atoms in der Punktgruppe des Methans (Td) in jeweils einer irreduziblen Darstellung wiederfinden (s in a1 und p in t2). Solche Dinge wollen wir jetzt systematischer angehen. Wir ordnen dabei die fortgeschrittenen Lehrinhalte Schwerpunktthemen zu, deren Relevanz der aktuellen gesellschaftlichen Diskussion entspringt (Treibhausgase, Energieerzeugung, -speicherung und -umwandlung, Lichterzeugung, Elektromobilität), zumindest aber wichtige Aspekte schulischer Konzepte aufgreift (Donor-Akzeptor-Modell) oder für das wissenschafliche Weltbild eines gebildeten Staatsbürgers wichtig sind (aerobes Leben, Biokatalyse).
Unsere Diskussion beginnt mit elektrostatischen Modellen einschließlich des Kristallfeldmodells.
NaCl und MgO bilden sich in stark exothermer Reaktion, die Standardbildungsenthalpien betragen −411 und −602 kJ mol−1. Wir diskutieren, warum das so ist, um die Edelgasregel auf den Punkt zu bringen. Danach sollte uns klar sein, warum es kein NaCl2 gibt. Grundlage ist das Kapitel „Die Ionenbindung“ im AC1-Skript.
Wir schauen uns die Strukturtypen ionischer Verbindungen aus der Grundvorlesung wiederholend an (Kapitel „ Feststoffe“ im AC1-Skript).
In diesem Abschnitt erweitern wir die einführende Behandlung der kovalenten Bindung der Grundvorlesung (Kapitel „ Die kovalente Bindung“ im AC1-Skript) um die Symmetrielehre.
Wir schauen auf das Chlormolekül, stellen die Lewisformel auf, fragen nach der Natur der einzelnen Elektronenpaare, konstruieren das MO-Schema und reden über die Lokalisierung von Wellenfunktionen.
Stickstoff ist viel reaktionsträger, als es einfache Bindungsmodelle nahelegen. Wird die Lewis-Formulierung betrachtet, so könnte man erwarten, dass N2 ähnlich bereitwillig Additionsreaktionen zeigt wie Ethin. Auch als Base oder Ligand könnte das N2-Molekül gesehen werden, wenn die Verwandtschaft mit Ammoniak betont wird. Warum trifft nichts von alledem zu? Wir diskutieren das MO-Schema des N2-Moleküls, benutzen dann aber die Lokalisierung nach dem NBO-Formalismus, um die s- und p-Orbitalbeteiligung an den einzelnen Orbitalen abzuleiten.
Auch der zweite Luftbestandteil, Sauerstoff, ist hinsichtlich der Bindungsbeschreibung nicht unkritisch. Hier ist der Paramagnetismus zu erklären, was mit Hilfe des MO-Modells gelingt.
Fließschema zur Ermittlung der häufigsten Punktgruppen (als pdf):
Wir stellen das MO-Schema für Methan auf. Einzelschritte: Darstellung der Valenzschale des C-Atoms und der vier H-Atome im Rahmen der Gruppentheorie. Arbeitsmaterialien hierzu:
Charaktertafel für die Punktgruppe Td:
| Td | E | 8C3 | 3C2 | 6S4 | 6σd | |||
|---|---|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | 1 | x2 + y2 + z2 | ||
| A2 | 1 | 1 | 1 | −1 | −1 | x2 − y2 | ||
| E | 2 | −1 | 2 | 0 | 0 | (2z2 − x2 − y2, x2 − y2) | ||
| T1 | 3 | 0 | −1 | 1 | −1 | (Rx, Ry, Rz) | ||
| T2 | 3 | 0 | −1 | −1 | 1 | (x, y, z) | (xy, yz, zx) |

Das MO-Schema von Methan (als pdf):
Wir machen uns am Beispiel von HF die zwei Schritte klar, mit denen man im MO-Schema eine nachrangige Wechselwirkung konstruiert: (1) zuerst wird anhand ähnlicher Orbitalenergien die dominante Wechselwirkung berücksichtigt – hier die H(1s)-F(2pz)-Überlappung, wenn z als Bindungsachse gewählt wird. Anschließend wird (2) im Sinne einer Störungsbetrachtung die nachrangige, aber symmetrieerlaubte Überlappung konstruiert – hier die H(1s)-F(2s)-Überlappung, durch die das stabile Orbital aus Schritt 1 (1 σ) weiter stabilisiert und das unstabilere (2 σ) weiter destabilisiert wird.
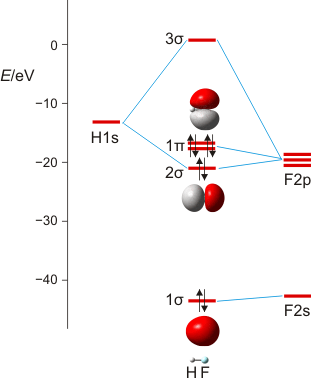
MO-Schema für HF; Ladung auf F nach Mulliken-Populationsanalyse: −0.43 e (technische Anmerkung: rmp2/6-31g(d,p)//rmp2/aug-cc-pvqz, bei F über α- und β-Spins gemittelt)
Anschließend die VB-Betrachtung: Lokalisierung der MOs ergibt als Fluor-Beitrag zur Bindung ein Orbital mit 15% s- und 85% p-Charakter.
Charaktertafel für C2v:
| C2v | E | C2 | σv | σv' | |||
|---|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | z | x2, y2, z2 | |
| A2 | 1 | 1 | −1 | −1 | Rz | xy | |
| B1 | 1 | −1 | 1 | −1 | x, Ry | zx | |
| B2 | 1 | −1 | −1 | 1 | y, Rx | yz |
Wir wählen das Koordinatensystem so, dass σv' in der Molekülebene liegt.
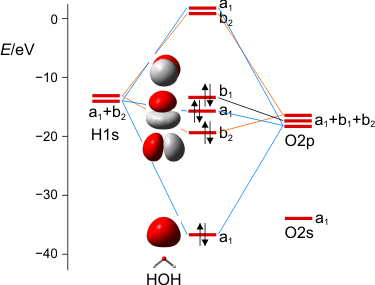
MO-Schema des Wasser-Moleküls.
Wir diskutieren, warum das nichtbindende Orbital im Molekül gegenüber dem Atom destabilisiert ist, vor allem aber, wie wir die drei a1-Zustände zu drei MOs kombinieren können. Man beachte hierbei, dass die beiden Zustände bei Wasserstoff nicht jeweils für ein 1s-Orbital eines Wasserstoffatoms stehen, sondern für die symmetrische (a1) und antisymmetrische (b2) Kombination der beiden AOs.
Zum Schluss werden wir die MOs des Wassers lokalisieren und über den Zusammenhang mit der VB-Vorstellung reden. Dabei ergeben sich Bindungen, zu denen das O-Atom jeweils 25% s- und 75% p-Charakter beisteuert. Es wird besprochen, was das für das VSEPR-Modell zu bedeuten hat.
Das Ammoniak-Molekül ist gut geeignet, um die umfassende Bedeutung der Symmetriebeschreibung zu demonstrieren. Das Molekül hat C3v-Symmetrie. Die Charaktertafel der Punktgruppe C3v wird mehrmals benutzt: (1) Um qualitativ die Symmetrieeigenschaften der MOs zu erfassen, (2) um die Zahl der N-H-Valenzschwingungen vorherzusagen, (3) um alle Molekülschwingungen vorherzusagen. Vorab legen wir ein Koordinatensystem fest; wir wählen eines, dessen Ursprung im N-Atom liegt und bei dem z auf den Betrachter zuweist:
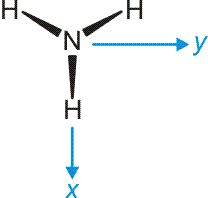
Nun zuerst das qualitative MO-Diagramm. Wir gehen ganz formal vor und machen das Ergebnis erst anschließend anhand einer computerchemischen Rechnung anschaulich. Im Anschluss an die Charaktertafel ist zusammengestellt, wie die Stickstoff-Valenzorbitale N(2s) und N(2p) sowie die Gruppe der drei H(1s)-Orbitale in C3v transformieren.
| C3v | E | 2C3 | 3σv | |||
|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | z | x2 + y2, z2 | |
| A2 | 1 | 1 | −1 | Rz | ||
| E | 2 | −1 | 0 | (x, y) (Rx, Ry) | (x2 − y2, xy) (xz, yz) |
| C3v | E | 2C3 | 3σv |
|---|---|---|---|
| N(2s) | 1 | 1 | 1 |
| N(2p) | 3 | 0 | 1 |
| 3 H(1s) | 3 | 0 | 1 |
Das Ergebnis der Analyse: N(2s) ist ein a1-Orbital. Auch die übrigen beiden Objekte enthalten die Rasse A1. Wenn diese von 3 0 1 subtrahiert wird, verbleibt 2 −1 0, also E. Die 7 Atomorbitale ergeben also 7 Molekülorbitale: 3 × a1 und 2 × e. Bei der Konstruktion eines qualitativen MO-Schemas beachten wir bei den a1-Orbitalen, wie man drei Orbitale korrekt kombiniert (diesselbe Frage tritt zum Beispiel bei HF auf, wo ein H(1s)-Orbital symmetrieerlaubt mit F(2s) und F(2pz) wechselwirken kann, ferner völlig analog bei Wasser). Wie sich diese Überlegungen in der quantitativen Behandlung wiederfinden, sehen Sie weiter unten.
Der zweite Punkt ist die Vorhersage, wieviele Valenzschwingungen im IR-Spektrum erwartet werden dürfen. Es ist sinnvoll, das Vorgehen zu besprechen, auch wenn gleich Punkt 3 folgt (alle Schwingungen), da eine vollständige Analyse oft sehr zeitraubend und nervtötend ist, man aber nur die Valenzschwingungen wissen will. Das typische Lehrbuchbeispiel hierzu ist die Frage, ob Pentacarbonyleisen(0) D3h- oder C4v-Symmetrie hat. Hierzu bestimmt man in beiden Punktgruppen die Zahl der IR-aktiven C-O-Valenzschwingungen und vergleicht mit dem Experiment. Für Ammoniak geht das so: man betrachtet die Valenzschwingung als Vektor von N zu H und fragt, wie die drei Vektoren in C3v transformieren, nämlich:
| C3v | E | 2C3 | 3σv |
|---|---|---|---|
| Γvalenz | 3 | 0 | 1 |
… wie die drei H(1s)-Orbitale, die ja den Vektorspitzen äquivalent sind. Γvalenz transformiert also wie A1 + E, wir erwarten demnach zwei Valenzschwingungen, also zwei Banden im typischen Bereich oberhalb 3000 cm−1. Die Analyse des kompletten Schwingungsspektrums ist erheblich mühsamer. Wir werden sehen, dass es für ein Molekül wie Fe(CO)5, das mit 11 Atomen über 33 Freiheitsgrade verfügt, keine rechte Freude macht.
Bei Ammoniak ist es halbwegs überschaubar. Zuerst eine allgemein gültige Überlegung. Eine Schwingung hat mit einer Molekültranslation und einer Rotation gemeinsam, dass die Atome um einen bestimmten Vektor mit den Komponenten xyz verschoben werden. N Atome haben insgesamt 3N Freiheitsgrade. Werden (bei einem nichtlinearen Molekül) für die Translation und die Rotation jeweils 3 Freiheitsgrade abgezogen, verbleiben 3N−6 Schwingungsfreiheitsgrade. Um diese zu ermitteln, werden bei jedem Atom die drei Basisvektoren x, y und z transformiert.
Für Ammoniak mit N = 4 sind dies 12 Vektoren. Deren Transformation wird nun betrachtet, und zwar als reduzible Darstellung Γtot:
| C3v | E | 2C3 | 3σv | |||
|---|---|---|---|---|---|---|
| Γtot | 12 | 0 | 2 |
Der Charakter 0 unter 2C3 ergibt sich als 3 × 0 für die Koordinaten der H-Atome + (−½ −½ +1) für xyz des N-Atoms. Der Charakter 2 unter 3σv errechnet sich aus 2 × 0 für die H-Atome außerhalb der Spiegelebene + 1 (xN) −1 (yN) + 1 (zN) + 1 (xH) −1 (yH) + 1 (zH), wenn die Spiegelebene in xz betrachtet wird.
Als nächstes werden nun die Zusatzangaben der Charaktertafel genutzt. Um die Rassen der Molekültranslation und -rotation zu ermitteln, werden die Einträge x, y und z (Translation) und Rx, Ry und Rz (Rotation) gesucht. Die sich dabei ergebenden Rassen für die Translation (A1 + E) und die Rotation (A2 + E) werden von Γtot abgezogen. Es bleibt Γvib übrig. Die reduzible Darstellung Γvib (6 0 2) lässt sich nun zusammensetzen aus 2 A1 + 2 E (man kann das durch Probieren herausbekommen oder mit einer Reduktionsformel). Beide Rassen sind IR-aktiv (sie transformieren wie x, y, z), es sollten also 4 Banden beobachtet werden – zusätzlich zu den beiden Valenzschwingungen noch zwei weitere bei wahrscheinlich niedriger Energie.
Für NH3 werden im Standardwerk von Herzberg zwei schwache Banden bei 3414 (e) und 3336 cm−1 (a1) angegeben, außerdem starke Banden bei 1628 (e) und 968 cm−1 (a1). In der nachfolgenden Tabelle bedeutet „ab initio“ das Ergebns einer MP2/6-311+G(2d,p)-Rechnung, die Spalte „×0.965“ korrigiert mit einem üblichen Faktor, der berücksichtigt, dass berechnete Frequenzen aufgrund der Annahme einer harmonischen Schwingung meist zu hoch sind. In der Spalte „Intensität“ ist das Ergebnis der Rechnung angegeben.
| exp./cm−1 | ab initio | ×0.965 | Intensität/% | |
|---|---|---|---|---|
| e | 3414 | 3646 | 3518 | 4.5 |
| a1 | 3336 | 3499 | 3377 | 1.3 |
| e | 1628 | 1679 | 1620 | 24 |
| a1 | 968 | 1051 | 1014 | 100 |
Die Tabelle leitet zum computerchemischen Teil über. Sowohl die MO-Betrachtung als auch die Ausführungen zum IR-Spektrum werden erheblich plastischer, wenn sie durch eine Rechnung konkretisiert werden. Wir besprechen hier kurz den Praktikumsversuch, bei dem Sie diese Rechnungen selbst ausführen. Zur Übung machen wir genau das auch und erzeugen einige Dateien, darunter die folgenden, die wir dann mit Hilfe von GaussView visualisieren:
| Datei | enthält Information zu |
|---|---|
| nh3_opt_mp2.out | Energien der MOs |
| nh3_opt_mp2.chk | Konturen der MOs für Graphikprogramme |
| nh3_freq_nbo_mp2.chk | NBOs |
| nh3_freq_nbo_mp2.out | Schwingungen |
„NBOs“ (natürliche Bindungsorbitale) stellen eine Möglichkeit dar, MOs unter Aufgabe der Energieinformation in – wenn möglich – 2-Elektronen-2-Zentren-Bindungen zu lokalisieren.
Noch einige Zahlenangaben, um im ersten Schritt ein MO-Diagramm zu zeichnen: Auf dem gewählten theoretischen Niveau hat das H(1s)-Orbital die Energie −13.6 eV, das N(2s)-Orbital −25.7eV (als Mittelwert aus −31.6 [α-Spin-Elektron] und −19.8 eV [β-Spin-Elektron]), die entarteten N(2p)-Orbitale −15.5 eV. Für die Valenzelektronen des NH3-Moleküls ergibt sich: 1a1 −31.0 eV, 1e −17.1 eV, 2a1 −11.6 eV. Um diese in eV angegebenen Energiewerte der Rechnung zu entnehmen, wird die übliche Angabe in atomaren Einheiten („Hartree“) durch 96.485 dividiert. Die Energie der unbesetzten Orbitale 2.7 (2e) und 4.3 eV (3a1) muss man nicht ernst nehmen. Das Ergebnis:
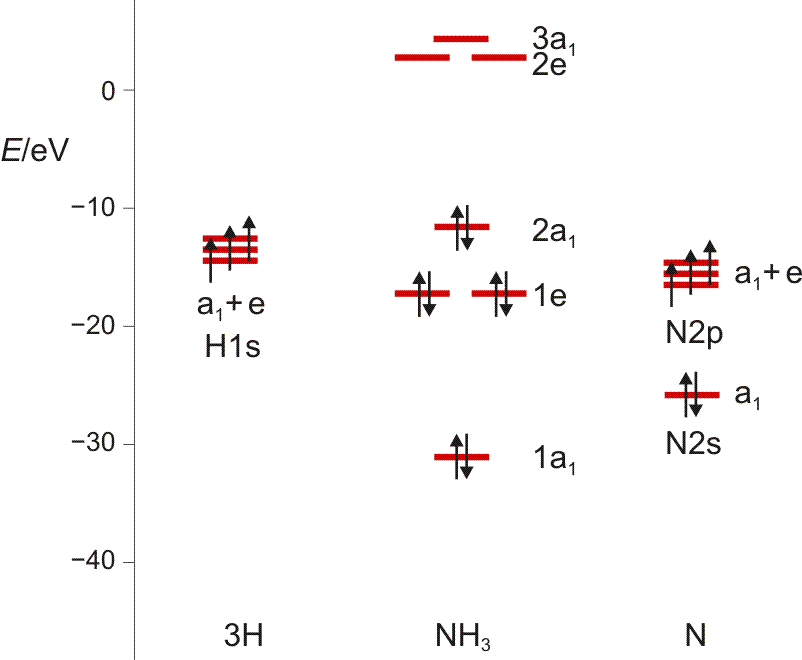
Wir schauen vor allem auf die Verteilung der a1-MOs entlang der Energieachse, und stellen den Bezug zu HF und H2O her. (Damit Sie in das Schema hineinmalen können, hier ein pdf.)
Wenden Sie jetzt das Gelernte an, um eine stereochemische Frage zu beantworten: Ammoniak könnte doch auch trigonal-planar sein, so wie BH3. Könnte man dies IR-spektroskopisch entscheiden? Berücksichtigen Sie nur die N-H-Valenzschwingungen. (Wenn Sie herausbekommen haben, dass diese entsprechend 3 0 1 3 0 1 transformieren, haben Sie bis hierhin alles richtig gemacht und es kann weitergehen.)
| D3h | E | 2C3 | 3C2 | σh | 2S3 | 3σv | |||
|---|---|---|---|---|---|---|---|---|---|
| A1′ | 1 | 1 | 1 | 1 | 1 | 1 | x2 + y2, z2 | ||
| A2′ | 1 | 1 | −1 | 1 | 1 | −1 | Rz | ||
| E′ | 2 | −1 | 0 | 2 | −1 | 0 | (x, y) | x2− y2, xy | |
| A1′′ | 1 | 1 | 1 | −1 | −1 | −1 | |||
| A2′′ | 1 | 1 | −1 | −1 | −1 | 1 | z | ||
| E′′ | 2 | −1 | 0 | −2 | 1 | 0 | (Rx, Ry) | (xz, yz) |
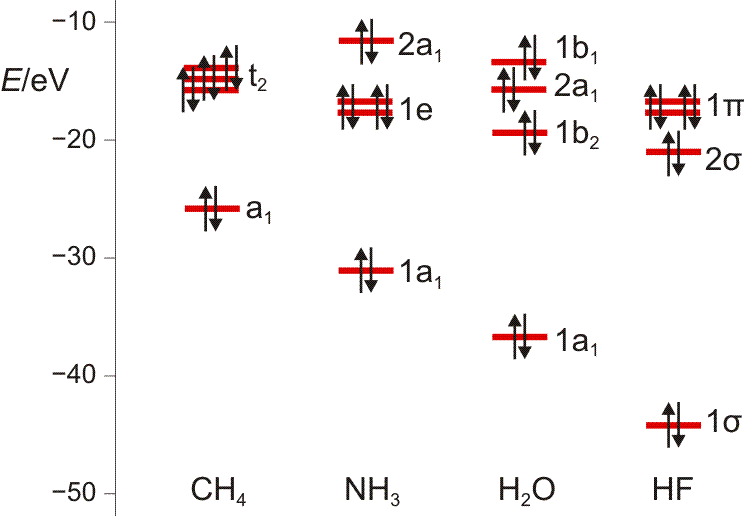
Es ist übrigens recht lehrreich, die MO-Schemata von Methan, Ammoniak, Wasser und Fluorwasserstoff im Zusammenhang zu sehen und die „Spuren“ von Dingen wie der Elektronegativität, der Basizität oder der Ligandeigenschaften dieser Moleküle zu suchen:
Pentacarbonyleisen(0) ist eine wasserklare Flüssigkeit, deren IR-Spektrum im C-O-Valenzschwingungsbereich zwei Banden aufweist: eine schwächere bei 2034 und eine stärkere bei 2013 cm−1. Anhand dieses Befunds lässt sich die Struktur wahrscheinlich machen. Spielen Sie hierzu zwei Möglichkeiten durch: wieviele Valenzschwingungen sind bei trigonal-bipyramidalem Aufbau zu erwarten (D3h, benutzen Sie die Charaktertafel oben), wieviele bei quadratisch-pyramidaler Struktur (C4v)? Beachten Sie, dass IR-aktive Schwingungen wie die Koordinatenachsen x, y, z transformieren, bei C4v wären also A1 und E IR-aktiv, bei D3h A2′′ und E′.
| C4v | E | 2C4 | C2 | 2σv | 2σd | |||
|---|---|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | 1 | z | x2 + y2, z2 | |
| A2 | 1 | 1 | 1 | −1 | −1 | Rz | ||
| B1 | 1 | −1 | 1 | 1 | −1 | x2 − y2 | ||
| B2 | 1 | −1 | 1 | −1 | 1 | xy | ||
| E | 2 | 0 | −2 | 0 | 0 | (x, y) (Rx, Ry) | (xz, yz) |
Ausführlichere Informationen finden Sie im Skript zur Vorlesung Koordinationschemie (Kapitel „ Carbonyl-Metall-Komplexe“).
Wenn Sie die folgenden Aufgaben zur Gruppentheorie lösen können, ist für die Klausur alles gut:
Wir betrachten das Wassermolekül. Dazu erhalten Sie die Charaktertafel für C2v. Sie sehen dort außer E die Symmetrieelemente C2, σv und σv'. Die Molekülebene falle mit σv' zusammen. Zeichnen Sie die übrigen Symmetrieelemente ein.
Schauen Sie als nächstes die Molekülorbitale des Wasser-Valenzbereichs an. Sie sind so gezeichnet, dass man die Beiträge der Atomorbitale gut erkennen kann. Bestimmen Sie nun mit Hilfe der Charaktertafel die jeweilige Rasse für jedes Orbital.
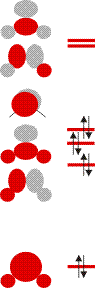
Verwenden Sie anschließend wieder die Charaktertafel, um die Zahl und Rasse der O-H-Valenzschwingungen zu bestimmen. Welche davon sind im IR-Spektrum beobachtbar? Skizzieren Sie, welche Schwingung durch die jeweilige Rasse beschrieben wird.
Eine Übung aus dem Bereich der Carbonyl-Metall-Komplexe: Das tetraedrische [Ni(CO)4] ist Td-symmetrisch. Im C-O-Valenzschwingungsbereich wird eine Bande bei 2060 cm−1 beobachtet. Verwenden Sie die Charaktertafel der Punktgruppe Td, um diese Beobachtung zu erklären.
Noch einmal C2v: Isolektronisch mit [Ni(CO)4] ist [Fe(CO)2(NO)2]. Der Ersatz zweier Carbonyl- durch Nitrosylliganden erniedrigt die Symmetrie. Im IR-Spektrum werden im Bereich der N-O- und C-O-Valenzschwingungen zwei Bandenpaare beobachtet: bei 2087 und 2034 cm−1 sowie bei 1810 und 1756 cm−1. Ordnen Sie die Bandenpaare den Liganden zu und finden Sie mit Hilfe der Charaktertafel heraus, wieso es sich um Bandenpaare handelt.
Wir formulieren im Einklang mit der Oktettregel: SO2, SOCl2, H2SO3, H2SO4 und ähnliche Moleküle, die auch in aktuellen Lehrbüchern oft noch mit mehr als einem Elektronenoktett formuliert werden, obwohl keine nennenswerte d-Orbitalbeteiligung vorliegt. Wir achten darauf, dass zum Beispiel bei H2SO3 eine ungefähr doppelt so große Bindungsordnung der S-O- im Vergleich zur S-OH-Bindung zum Ausdruck kommt. In der Grundvorlesung wird dieser Abschnitt im Kapitel „Chalkogene“ behandelt.
Die Oktettregel gilt auch bei I3−, den Xenonhalogeniden, Interhalogenverbindungen wie ClF3, und Halogeniden von Nichtmetallen in deren höchster Oxidationsstufe wie PF5 und SF6. Wir machen uns klar, dass der Begriff „Hypervalenz“ Blödsinn ist – hier ist nichts „hyper“. (In der Grundvorlesung wird auch dieser Abschnitt im Kapitel „Chalkogene“ behandelt.)
Zum Schluss dieses Kapitels behandeln wir auch die koordinative Bindung durch ein Orbitalmodell und erweitern damit die elektrostatische Betrachtung vom Beginn der Vorlesung. Wir verwenden zu Beginn den Abschnitt „Aqua-Komplexe“ des AC3-Skripts, um die Bindung in Amminboran im Vergleich mit Ethan zu untersuchen, anschließend das [AlCl4]−-Ion. Dann schauen wir noch einmal in das Kapitel „Die Elektronenstruktur von Koordinationsverbindungen“), um im Rahmen einer MO-Betrachtung eine Beschränkung des Kristallfeldmodells zu überwinden. Es geht um …
Spektrenvergleich: [Cr(H2O)6]3+ und [Cr(OH)6]3− – was ist faul an der rein elektrostatischen Betrachtung der Kristallfeldtheorie? Weiter geht es um: MO-Schema eines oktaedrischen Komplexes, π-Effekte von Liganden, NO: Botenstoff in der Biologie und π-saurer Ligand; spektrochemische Reihe, Bioliganden
Vorübungen zu den thermodynamischen Betrachtungen: Warum löst sich NaCl endotherm in Wasser? Warum lässt sich aus Kohle und Eisenoxid durch Erhitzen Eisen gewinnen? — Vielleicht überlegen Sie schon 'mal. Anschließend: Massenwirkungsgesetz, Stabilität eines Komplexes, Gleichgewichtskonstante und wichtige thermodynamische Größen (Enthalpie, Entropie, freie Enthalpie), Chelateffekt. In den einführenden Vorlesungen wurden diese Fragen angeschnitten (1) am Schluss des Kapitels „Die Ionenbindung“ im AC1-Skript und (2) im Kapitel „Massenwirkungsgesetz und Komplexbildung“ im AC3-Skript.
Inert und labil, Racemattrennung bei optisch aktiven Komplexen, Ligandsubstitution, Ligandfeldstabilisierungsenergie – hier greifen wir Aspekte auf, die in den Kapiteln „Geschwindigkeit und Mechanismus der Ligandsubstitution“ und „Isomerie“ im AC3-Skript behandelt wurden.
Nernstsche Gleichung, elektrochemisches Potential und Komplexbildungskonstante, Stabilität von Oxidationsstufen – hier noch einmal das AC3-Skript, und zwar „Thermodynamik und Mechanismen von Redoxreaktionen“.
Lehrbücher der Anorganischen Chemie für Fortgeschrittene. Eine Liste mit Angaben zu Buchbesprechungen finden bei den Literaturempfehlungen für die Vorlesung "Einführung in die Koordinationschemie".