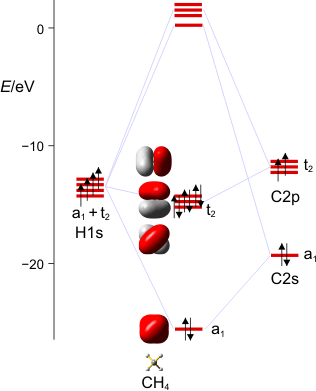
Das MO-Schema von Methan (als pdf):
Einschub in der Vorlesung Koordinationschemie (AC3) und, bis zur vollständigen Umsetzung der neuen Lehrerprüfungsordnung, in der begleitenden Vorlesung zum Forschungspraktikum für Lehramtstudierende (LAF-Praktikum).
Lehramtstudierende kommen zum ersten Mal im Rahmen der Vorlesung Koordinatonschemie mit der Symmetrielehre in Kontakt (was sind t2g-Orbitale?). Bachelorstudenten, die diese Vorlesung ebenfalls hören, sind im vorangehenden Semester in die Symmetrielehre eingeführt worden. In diesem Schnellkurs wird die Symmetrielehre auf die Inhalte beschränkt, die für die Lehramtausbildung wichtig sind, das heißt vor allem, dass die mathematische Ableitung fehlt.
Prüfen Sie hier, ob Ihr Browser das Skript korrekt darstellt.
Sie können dort, wo es angegeben ist, einzelne Graphiken als pdf herunterladen, wenn Sie wollen, aber auch den gesamten Text.
Es werden die Grundlagen vermittelt, um im Rahmen der LAF-Vorlesung die Bindung in einfachen, schulrelevanten Molekülen wie Methan behandeln zu können. Im Bereich der Koordinationschemie geht es vor allem um oktaedrische Komplexe und deren verzerrte Formen.
Wir machen uns zu Beginn klar, was Symmetrie ist. Anschließend drücken wir die verschiedenen Symmetrieoperationen in Schönflies' Schreibweise aus. Die von der Schule bekannten Operationen i und σ, dann die Drehachsen Cn und schließlich die Drehspiegelachsen Sn (n ist jeweils die Zähligkeit der Achse). Wir lernen dann Symmetriegruppen als Ansammlung miteinander verträglicher Operationen kennen (und nehmen wegen des Gruppenbegriffs noch die Identität E als Symmetrieoperation hinzu). Dann beschränken wir uns auf Gruppen, die bei Molekülen besonderes häufig vorkommen und verwenden ein Fließschema, um diese häufigsten Punktgruppen zu ermitteln (auch als pdf):
Fließschema zur Ermittlung der häufigsten Punktgruppen
Wir stellen das MO-Schema für Methan auf. Einzelschritte: Darstellung der Valenzschale des C-Atoms und der vier H-Atome im Rahmen der Gruppentheorie. Arbeitsmaterialien hierzu:
Charaktertafel für die Punktgruppe Td:
| Td | E | 8C3 | 3C2 | 6S4 | 6σd | |||
|---|---|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | 1 | x2 + y2 + z2 | ||
| A2 | 1 | 1 | 1 | −1 | −1 | x2 − y2 | ||
| E | 2 | −1 | 2 | 0 | 0 | (2z2 − x2 − y2, x2 − y2) | ||
| T1 | 3 | 0 | −1 | 1 | −1 | (Rx, Ry, Rz) | ||
| T2 | 3 | 0 | −1 | −1 | 1 | (x, y, z) | (xy, yz, zx) |

Das MO-Schema von Methan (als pdf):
Wir machen uns am Beispiel von HF die zwei Schritte klar, mit denen man im MO-Schema eine nachrangige Wechselwirkung konstruiert: (1) zuerst wird anhand ähnlicher Orbitalenergien die dominante Wechselwirkung berücksichtigt – hier die H(1s)-F(2pz)-Überlappung, wenn z als Bindungsachse gewählt wird. Anschließend wird (2) im Sinne einer Störungsbetrachtung die nachrangige, aber symmetrieerlaubte Überlappung konstruiert – hier die H(1s)-F(2s)-Überlappung, durch die das stabile Orbital aus Schritt 1 (1 σ) weiter stabilisiert und das unstabilere (2 σ) weiter destabilisiert wird.
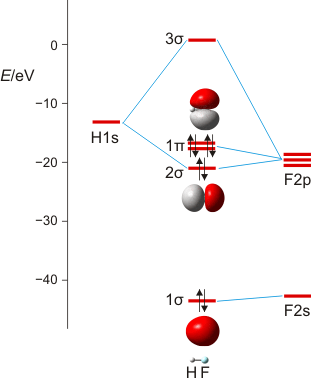
MO-Schema für HF; Ladung auf F nach Mulliken-Populationsanalyse: −0.43 e (technische Anmerkung: rmp2/6-31g(d,p)//rmp2/aug-cc-pvqz, bei F über α- und β-Spins gemittelt)
Anschließend die VB-Betrachtung: Lokalisierung der MOs ergibt als Fluor-Beitrag zur Bindung ein Orbital mit 15% s- und 85% p-Charakter.
Charaktertafel für C2v:
| C2v | E | C2 | σv | σv' | |||
|---|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | z | x2, y2, z2 | |
| A2 | 1 | 1 | −1 | −1 | Rz | xy | |
| B1 | 1 | −1 | 1 | −1 | x, Ry | zx | |
| B2 | 1 | −1 | −1 | 1 | y, Rx | yz |
Wir wählen das Koordinatensystem so, dass σv' in der Molekülebene liegt.
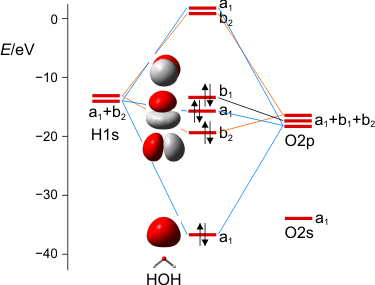
MO-Schema des Wasser-Moleküls.
Wir diskutieren, warum das nichtbindende Orbital im Molekül gegenüber dem Atom destabilisiert ist, vor allem aber, wie wir die drei a1-Zustände zu drei MOs kombinieren können. Man beachte hierbei, dass die beiden Zustände bei Wasserstoff nicht jeweils für ein 1s-Orbital eines Wasserstoffatoms stehen, sondern für die symmetrische (a1) und antisymmetrische (b2) Kombination der beiden AOs.
Zum Schluss werden wir die MOs des Wassers lokalisieren und über den Zusammenhang mit der VB-Vorstellung reden. Dabei ergeben sich Bindungen, zu denen das O-Atom jeweils 25% s- und 75% p-Charakter beisteuert. Es wird besprochen, was das für das VSEPR-Modell zu bedeuten hat.
Das Ammoniak-Molekül ist gut geeignet, um die umfassende Bedeutung der Symmetriebeschreibung zu demonstrieren. Das Molekül hat C3v-Symmetrie. Die Charaktertafel der Punktgruppe C3v wird mehrmals benutzt: (1) Um qualitativ die Symmetrieeigenschaften der MOs zu erfassen, (2) um die Zahl der N-H-Valenzschwingungen vorherzusagen, (3) um alle Molekülschwingungen vorherzusagen. Vorab legen wir ein Koordinatensystem fest; wir wählen eines, dessen Ursprung im N-Atom liegt und bei dem z auf den Betrachter zuweist:
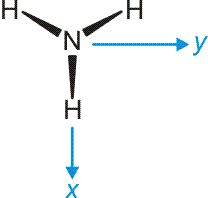
Nun zuerst das qualitative MO-Diagramm. Wir gehen ganz formal vor und machen das Ergebnis erst anschließend anhand einer computerchemischen Rechnung anschaulich. Im Anschluss an die Charaktertafel ist zusammengestellt, wie die Stickstoff-Valenzorbitale N(2s) und N(2p) sowie die Gruppe der drei H(1s)-Orbitale in C3v transformieren.
| C3v | E | 2C3 | 3σv | |||
|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | z | x2 + y2, z2 | |
| A2 | 1 | 1 | −1 | Rz | ||
| E | 2 | −1 | 0 | (x, y) (Rx, Ry) | (x2 − y2, xy) (xz, yz) |
| C3v | E | 2C3 | 3σv |
|---|---|---|---|
| N(2s) | 1 | 1 | 1 |
| N(2p) | 3 | 0 | 1 |
| 3 H(1s) | 3 | 0 | 1 |
Das Ergebnis der Analyse: N(2s) ist ein a1-Orbital. Auch die übrigen beiden Objekte enthalten die Rasse A1. Wenn diese von 3 0 1 subtrahiert wird, verbleibt 2 −1 0, also E. Die 7 Atomorbitale ergeben also 7 Molekülorbitale: 3 × a1 und 2 × e. Bei der Konstruktion eines qualitativen MO-Schemas beachten wir bei den a1-Orbitalen, wie man drei Orbitale korrekt kombiniert (diesselbe Frage tritt zum Beispiel bei HF auf, wo ein H(1s)-Orbital symmetrieerlaubt mit F(2s) und F(2pz) wechselwirken kann, ferner völlig analog bei Wasser). Wie sich diese Überlegungen in der quantitativen Behandlung wiederfinden, sehen Sie weiter unten.
Der zweite Punkt ist die Vorhersage, wieviele Valenzschwingungen im IR-Spektrum erwartet werden dürfen. Es ist sinnvoll, das Vorgehen zu besprechen, auch wenn gleich Punkt 3 folgt (alle Schwingungen), da eine vollständige Analyse oft sehr zeitraubend und nervtötend ist, man aber nur die Valenzschwingungen wissen will. Das typische Lehrbuchbeispiel hierzu ist die Frage, ob Pentacarbonyleisen(0) D3h- oder C4v-Symmetrie hat. Hierzu bestimmt man in beiden Punktgruppen die Zahl der IR-aktiven C-O-Valenzschwingungen und vergleicht mit dem Experiment. Für Ammoniak geht das so: man betrachtet die Valenzschwingung als Vektor von N zu H und fragt, wie die drei Vektoren in C3v transformieren, nämlich:
| C3v | E | 2C3 | 3σv |
|---|---|---|---|
| Γvalenz | 3 | 0 | 1 |
… wie die drei H(1s)-Orbitale, die ja den Vektorspitzen äquivalent sind. Γvalenz transformiert also wie A1 + E, wir erwarten demnach zwei Valenzschwingungen, also zwei Banden im typischen Bereich oberhalb 3000 cm−1. Die Analyse des kompletten Schwingungsspektrums ist erheblich mühsamer. Wir werden sehen, dass es für ein Molekül wie Fe(CO)5, das mit 11 Atomen über 33 Freiheitsgrade verfügt, keine rechte Freude macht.
Bei Ammoniak ist es halbwegs überschaubar. Zuerst eine allgemein gültige Überlegung. Eine Schwingung hat mit einer Molekültranslation und einer Rotation gemeinsam, dass die Atome um einen bestimmten Vektor mit den Komponenten xyz verschoben werden. N Atome haben insgesamt 3N Freiheitsgrade. Werden (bei einem nichtlinearen Molekül) für die Translation und die Rotation jeweils 3 Freiheitsgrade abgezogen, verbleiben 3N−6 Schwingungsfreiheitsgrade. Um diese zu ermitteln, werden bei jedem Atom die drei Basisvektoren x, y und z transformiert.
Für Ammoniak mit N = 4 sind dies 12 Vektoren. Deren Transformation wird nun betrachtet, und zwar als reduzible Darstellung Γtot:
| C3v | E | 2C3 | 3σv | |||
|---|---|---|---|---|---|---|
| Γtot | 12 | 0 | 2 |
Der Charakter 0 unter 2C3 ergibt sich als 3 × 0 für die Koordinaten der H-Atome + (−½ −½ +1) für xyz des N-Atoms. Der Charakter 2 unter 3σv errechnet sich aus 2 × 0 für die H-Atome außerhalb der Spiegelebene + 1 (xN) −1 (yN) + 1 (zN) + 1 (xH) −1 (yH) + 1 (zH), wenn die Spiegelebene in xz betrachtet wird.
Als nächstes werden nun die Zusatzangaben der Charaktertafel genutzt. Um die Rassen der Molekültranslation und -rotation zu ermitteln, werden die Einträge x, y und z (Translation) und Rx, Ry und Rz (Rotation) gesucht. Die sich dabei ergebenden Rassen für die Translation (A1 + E) und die Rotation (A2 + E) werden von Γtot abgezogen. Es bleibt Γvib übrig. Die reduzible Darstellung Γvib (6 0 2) lässt sich nun zusammensetzen aus 2 A1 + 2 E (man kann das durch Probieren herausbekommen oder mit einer Reduktionsformel). Beide Rassen sind IR-aktiv (sie transformieren wie x, y, z), es sollten also 4 Banden beobachtet werden – zusätzlich zu den beiden Valenzschwingungen noch zwei weitere bei wahrscheinlich niedriger Energie.
Für NH3 werden im Standardwerk von Herzberg zwei schwache Banden bei 3414 (e) und 3336 cm−1 (a1) angegeben, außerdem starke Banden bei 1628 (e) und 968 cm−1 (a1). In der nachfolgenden Tabelle bedeutet „ab initio“ das Ergebns einer MP2/6-311+G(2d,p)-Rechnung, die Spalte „×0.965“ korrigiert mit einem üblichen Faktor, der berücksichtigt, dass berechnete Frequenzen aufgrund der Annahme einer harmonischen Schwingung meist zu hoch sind. In der Spalte „Intensität“ ist das Ergebnis der Rechnung angegeben.
| exp./cm−1 | ab initio | ×0.965 | Intensität/% | |
|---|---|---|---|---|
| e | 3414 | 3646 | 3518 | 4.5 |
| a1 | 3336 | 3499 | 3377 | 1.3 |
| e | 1628 | 1679 | 1620 | 24 |
| a1 | 968 | 1051 | 1014 | 100 |
Die Tabelle leitet zum computerchemischen Teil über. Sowohl die MO-Betrachtung als auch die Ausführungen zum IR-Spektrum werden erheblich plastischer, wenn sie durch eine Rechnung konkretisiert werden. Wir besprechen hier kurz den Praktikumsversuch, bei dem Sie diese Rechnungen selbst ausführen. Zur Übung machen wir genau das auch und erzeugen einige Dateien, darunter die folgenden, die wir dann mit Hilfe von GaussView visualisieren:
| Datei | enthält Information zu |
|---|---|
| nh3_opt_mp2.out | Energien der MOs |
| nh3_opt_mp2.chk | Konturen der MOs für Graphikprogramme |
| nh3_freq_nbo_mp2.chk | NBOs |
| nh3_freq_nbo_mp2.out | Schwingungen |
„NBOs“ (natürliche Bindungsorbitale) stellen eine Möglichkeit dar, MOs unter Aufgabe der Energieinformation in – wenn möglich – 2-Elektronen-2-Zentren-Bindungen zu lokalisieren.
Noch einige Zahlenangaben, um im ersten Schritt ein MO-Diagramm zu zeichnen: Auf dem gewählten theoretischen Niveau hat das H(1s)-Orbital die Energie −13.6 eV, das N(2s)-Orbital −25.7eV (als Mittelwert aus −31.6 [α-Spin-Elektron] und −19.8 eV [β-Spin-Elektron]), die entarteten N(2p)-Orbitale −15.5 eV. Für die Valenzelektronen des NH3-Moleküls ergibt sich: 1a1 −31.0 eV, 1e −17.1 eV, 2a1 −11.6 eV. Um diese in eV angegebenen Energiewerte der Rechnung zu entnehmen, wird die übliche Angabe in atomaren Einheiten („Hartree“) durch 96.485 dividiert. Die Energie der unbesetzten Orbitale 2.7 (2e) und 4.3 eV (3a1) muss man nicht ernst nehmen. Das Ergebnis:
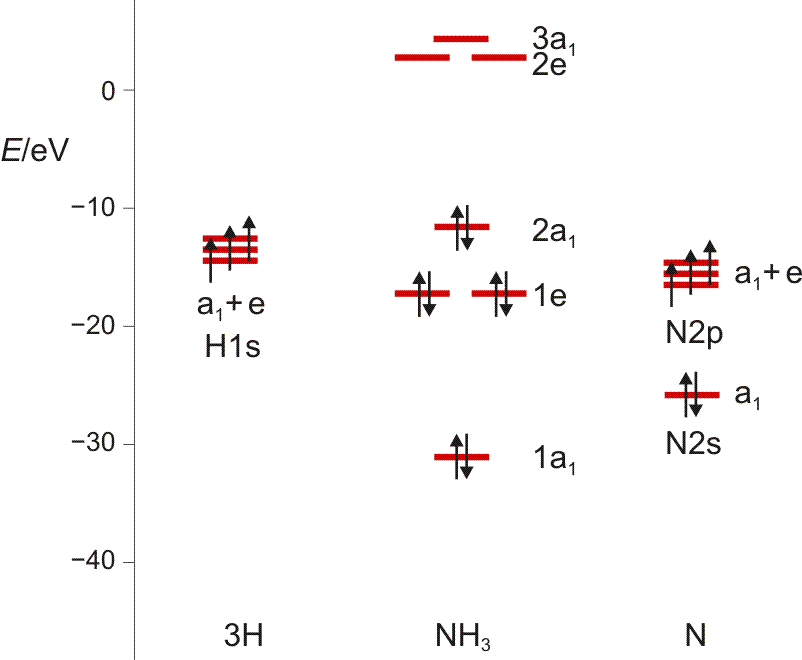
Wir schauen vor allem auf die Verteilung der a1-MOs entlang der Energieachse, und stellen den Bezug zu HF und H2O her. (Damit Sie in das Schema hineinmalen können, hier ein pdf.)
Wenden Sie jetzt das Gelernte an, um eine stereochemische Frage zu beantworten: Ammoniak könnte doch auch trigonal-planar sein, so wie BH3. Könnte man dies IR-spektroskopisch entscheiden? Berücksichtigen Sie nur die N-H-Valenzschwingungen. (Wenn Sie herausbekommen haben, dass diese entsprechend 3 0 1 3 0 1 transformieren, haben Sie bis hierhin alles richtig gemacht und es kann weitergehen.)
| D3h | E | 2C3 | 3C2 | σh | 2S3 | 3σv | |||
|---|---|---|---|---|---|---|---|---|---|
| A1′ | 1 | 1 | 1 | 1 | 1 | 1 | x2 + y2, z2 | ||
| A2′ | 1 | 1 | −1 | 1 | 1 | −1 | Rz | ||
| E′ | 2 | −1 | 0 | 2 | −1 | 0 | (x, y) | x2− y2, xy | |
| A1′′ | 1 | 1 | 1 | −1 | −1 | −1 | |||
| A2′′ | 1 | 1 | −1 | −1 | −1 | 1 | z | ||
| E′′ | 2 | −1 | 0 | −2 | 1 | 0 | (Rx, Ry) | (xz, yz) |
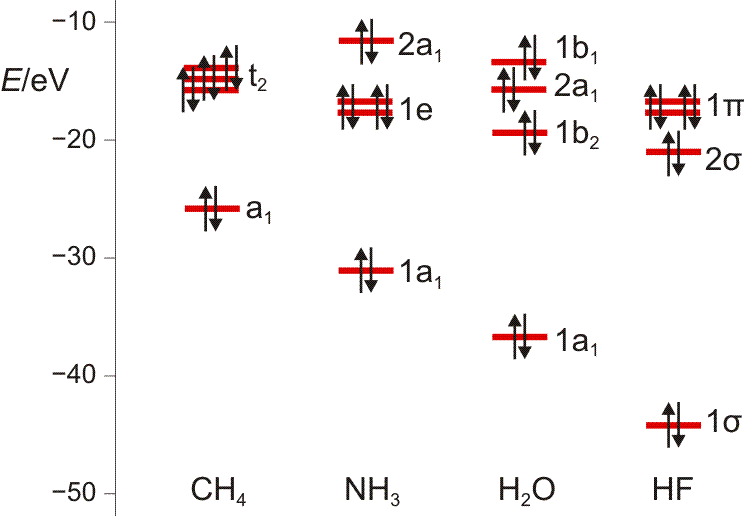
Es ist übrigens recht lehrreich, die MO-Schemata von Methan, Ammoniak, Wasser und Fluorwasserstoff im Zusammenhang zu sehen und die „Spuren“ von Dingen wie der Elektronegativität, der Basizität oder der Ligandeigenschaften dieser Moleküle zu suchen:
Pentacarbonyleisen(0) ist eine wasserklare Flüssigkeit, deren IR-Spektrum im C-O-Valenzschwingungsbereich zwei Banden aufweist: eine schwächere bei 2034 und eine stärkere bei 2013 cm−1. Anhand dieses Befunds lässt sich die Struktur wahrscheinlich machen. Spielen Sie hierzu zwei Möglichkeiten durch: wieviele Valenzschwingungen sind bei trigonal-bipyramidalem Aufbau zu erwarten (D3h, benutzen Sie die Charaktertafel oben), wieviele bei quadratisch-pyramidaler Struktur (C4v)? Beachten Sie, dass IR-aktive Schwingungen wie die Koordinatenachsen x, y, z transformieren, bei C4v wären also A1 und E IR-aktiv, bei D3h A2′′ und E′.
| C4v | E | 2C4 | C2 | 2σv | 2σd | |||
|---|---|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | 1 | z | x2 + y2, z2 | |
| A2 | 1 | 1 | 1 | −1 | −1 | Rz | ||
| B1 | 1 | −1 | 1 | 1 | −1 | x2 − y2 | ||
| B2 | 1 | −1 | 1 | −1 | 1 | xy | ||
| E | 2 | 0 | −2 | 0 | 0 | (x, y) (Rx, Ry) | (xz, yz) |
Ausführlichere Informationen finden Sie im Skript zur Vorlesung Koordinationschemie (Kapitel „ Carbonyl-Metall-Komplexe“).
Wenn Sie die folgenden Aufgaben zur Gruppentheorie lösen können, ist für die Klausur alles gut:
Wir betrachten das Wassermolekül. Dazu erhalten Sie die Charaktertafel für C2v. Sie sehen dort außer E die Symmetrieelemente C2, σv und σv'. Die Molekülebene falle mit σv' zusammen. Zeichnen Sie die übrigen Symmetrieelemente ein.
Schauen Sie als nächstes die Molekülorbitale des Wasser-Valenzbereichs an. Sie sind so gezeichnet, dass man die Beiträge der Atomorbitale gut erkennen kann. Bestimmen Sie nun mit Hilfe der Charaktertafel die jeweilige Rasse für jedes Orbital.
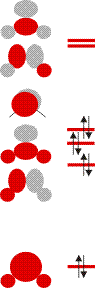
Verwenden Sie anschließend wieder die Charaktertafel, um die Zahl und Rasse der O-H-Valenzschwingungen zu bestimmen. Welche davon sind im IR-Spektrum beobachtbar? Skizzieren Sie, welche Schwingung durch die jeweilige Rasse beschrieben wird.
Eine Übung aus dem Bereich der Carbonyl-Metall-Komplexe: Das tetraedrische [Ni(CO)4] ist Td-symmetrisch. Im C-O-Valenzschwingungsbereich wird eine Bande bei 2060 cm−1 beobachtet. Verwenden Sie die Charaktertafel der Punktgruppe Td, um diese Beobachtung zu erklären.
Noch einmal C2v: Isolektronisch mit [Ni(CO)4] ist [Fe(CO)2(NO)2]. Der Ersatz zweier Carbonyl- durch Nitrosylliganden erniedrigt die Symmetrie. Im IR-Spektrum werden im Bereich der N-O- und C-O-Valenzschwingungen zwei Bandenpaare beobachtet: bei 2087 und 2034 cm−1 sowie bei 1810 und 1756 cm−1. Ordnen Sie die Bandenpaare den Liganden zu und finden Sie mit Hilfe der Charaktertafel heraus, wieso es sich um Bandenpaare handelt.